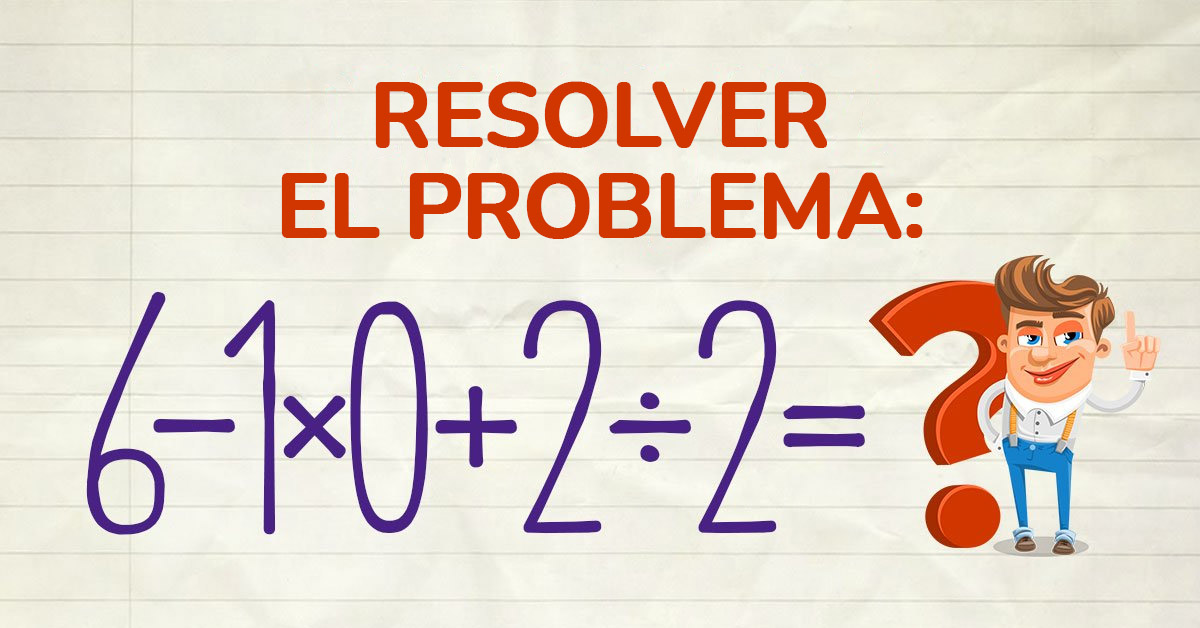A los adultos les gusta fingir que lo saben todo. Pero si un niño pide ayuda con las lecciones, antes recibirá un rechazo que una ayuda inteligible. Por supuesto, esos tíos y tías que estudiaron bien en la escuela seguramente resolverán cualquier acertijo matemático. ¿Pero hay muchos de ellos? Sugerimos comprobar.
Hoy, el consejo editorial de ¡Simplemente Genial! ofrece dos problemas completamente diferentes, pero extremadamente curiosos a la vez, que serán resueltos solo por aquellos que siempre han sido amigos de las matemáticas. Una buena forma de ponerte a prueba y descubrir si tu cerebro está en buena forma y si es capaz de resolver acertijos complicados.
 © Depositphotos
© Depositphotos
ACERTIJOS MATEMÁTICOS
Condiciones y preguntas
- Este ejemplo matemático aparentemente simple ha provocado una ola de discusiones en Internet. Esto se debe a que diferentes lectores obtuvieron diferentes respuestas. Algunos estaban convencidos de que la respuesta correcta era 5. Otros de que el resultado debería ser 1. Otros insistieron en que 7 era el resultado correcto. Pero, ¿Quién tiene razón? ¿O tal vez la respuesta es completamente diferente?
Problemas de matemáticas
- Si lograste lidiar fácilmente con la primera tarea, te ofrecemos un rompecabezas en el que debes activar la lógica y pensar con cuidado. Se rumorea que una vez, el sultán Saladino capturó a un caballero. El gobernante anunció que liberaría al prisionero y su caballo si recibía un rescate sólido de 30 mil monedas de oro. El caballero no tenía dinero ni parientes ricos, por lo que decidió hacer trampa.
«Oh, poderoso Saladino, no me das ninguna esperanza. En mi tierra natal, todo cautivo inteligente tiene la oportunidad de ser libre. Se le ofrece un rompecabezas. Si lo resuelve, queda libre, si no lo hace, el monto del rescate se duplica», dijo el dudoso guerrero.
A Saladino le encantaban los rompecabezas, así que aceptó la propuesta del prisionero.
«Está bien, que así sea. Este es tu problema. Mañana por la mañana se te entregarán doce monedas de aspecto idéntico y una balanza simple sin pesas. Una moneda será falsa. Pero nadie sabe si es más sencilla o más compleja que otras. Tendrás tres pesajes para determinar la falsificación. Si no puedes arreglártelas, tus asuntos están mal».
¿Cómo encontrar una moneda falsa entre 12 monedas en 3 pesajes? ¿Y es posible hacer esto?
Respuestas a acertijos
- Para resolver este ejemplo, debes recordar la regla de la escuela de que primero se realiza la multiplicación y la división, y solo luego la suma y la resta. Si es así, nuestro ejemplo tendrá la siguiente forma:
6 – 1 * 0 + 2/2 = 6 – 0 + 1 = 7. - El segundo problema tardará más. Es complicado por el hecho de que no sabemos por condición qué moneda es más pesada: la falsa o la real. También se desconoce si el caballero logró encontrar una respuesta antes de la mañana para salir. Intentemos hacerlo por él.
 © Depositphotos
© DepositphotosEl primer paso es dividir las monedas en 3 pilas iguales de 4 monedas. Pesemos los dos primeros lotes de monedas en la balanza. Si tienen el mismo peso, entonces tenemos suerte y la moneda falsa está en la tercera pila.
Luego pesamos dos monedas reales cualesquiera (cualquiera del primer y segundo lote) y dos monedas del último montón, donde acecha una falsa. Si nuevamente la balanza muestra igualdad, entonces la moneda falsa es una de las dos restantes (de las que no tocamos).
Por lo tanto, después del tercer paso, pesamos una de las monedas reales que ya conocemos con cualquiera de las dos restantes. Si vuelve a ser igual, entonces la moneda falsa es la que no tocamos. Si no hay igualdad, también se ha encontrado una falsificación. Al mismo tiempo, averiguaremos si es más pesada que la original o más ligera.
Si la desigualdad está en el segundo pesaje, entonces se encuentra un par con una falsificación. Encontrar una moneda falsa para el tercer pesaje es nuevamente fácil.
Si en el primer pesaje un grupo resultó ser más pesado, entonces la moneda falsa está entre estos primeros ocho. Quizás, en este caso, sería mejor numerar todas las monedas: la primera pila (pesada) – 1,2,3,4; el segundo (fácil) – 5,6,7,8; el tercero (real) – 9,10,11,12.
En el segundo paso, pesamos las monedas 1,9,10,11 y 2,3,4,5. Si hay un empate, entonces un falso 6,7 u 8. Además, después del primer pesaje, ya hemos aprendido que el segundo lote es más fácil. Esto significa que la falsificación es más ligera que la original. Por lo tanto, pesamos 6 y 7. Lo que es más fácil, eso es falso. Si es igual, la moneda falsa es 8.
Si después del segundo paso vimos que el grupo 1,9,10,11 es más pesado que el grupo 2,3,4,5, entonces el falso es 1 (más pesado) o 5 (más ligero). Basta con pesar, digamos, 1 y cualquier moneda real. Si 1 es más pesado, entonces es falso. Si es igual, entonces falso – 5.
Si el grupo 2,3,4,5 resulta ser más pesado, significa que la moneda falsa es más pesada, y se encuentra entre los 2,3,4. En este caso, pesamos, por ejemplo, 2 y 3. Lo que sea más pesado, eso es falso. Si es igual, entonces la moneda con el número condicional 4 será falsa.
 © Depositphotos
© Depositphotos
¡Fuh! El último problema resultó ser complicado. Por supuesto, podría simplificarse cambiando las condiciones iniciales, pero ¿sería justo? Espero que el caballero también lo solucione, porque claramente tenía más motivación. ¿O tal vez hay una forma más fácil?