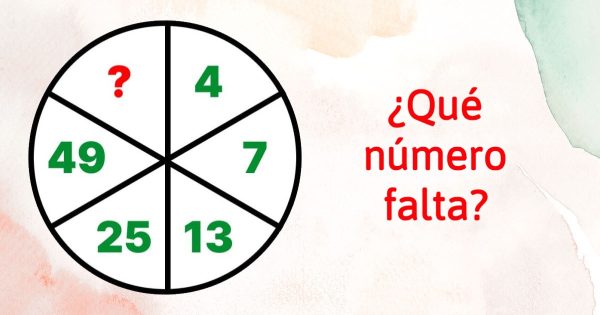
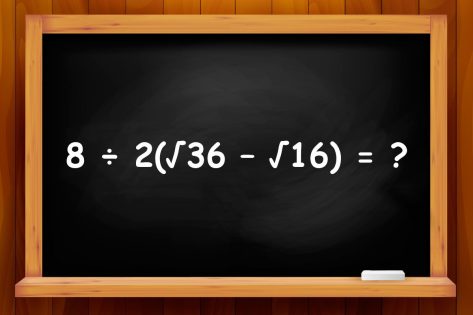El desarrollo del pensamiento de un matemático es imposible sin la resolución de problemas difíciles. Pero, ¿cómo saber qué tarea es difícil? Al fin y al cabo, la misma tarea resulta imposible para algunos y demasiado fácil para otros. Por eso nuestros rompecabezas y otras tareas casi siempre se toman del programa escolar. Si los escolares pueden resolverlo, nuestros lectores adultos también pueden encontrar la solución.
 © Depositphotos
© Depositphotos
Hoy la redacción de ¡Simplemente Genial! nos propone un viejo problema de la época soviética. Me pregunto cuánta gente se las arreglará para darle solución aquí a la suma de fracciones. ¿Será posible al menos adivinar qué camino seguir para llegar más rápido a la solución correcta?
DESARROLLAR EL PENSAMIENTO DE UN MATEMÁTICO
Por supuesto, mucha gente recordará que para hallar la suma de fracciones hay que llegar a un denominador común. Pero en la solución de nuestra tarea de hoy, esto es bastante difícil. Llevará tiempo y esfuerzo. Y siempre se puede cometer un error, que anulará todos los esfuerzos. Aun así, echa un vistazo a esta tarea y piensa qué puedes hacer con ella.
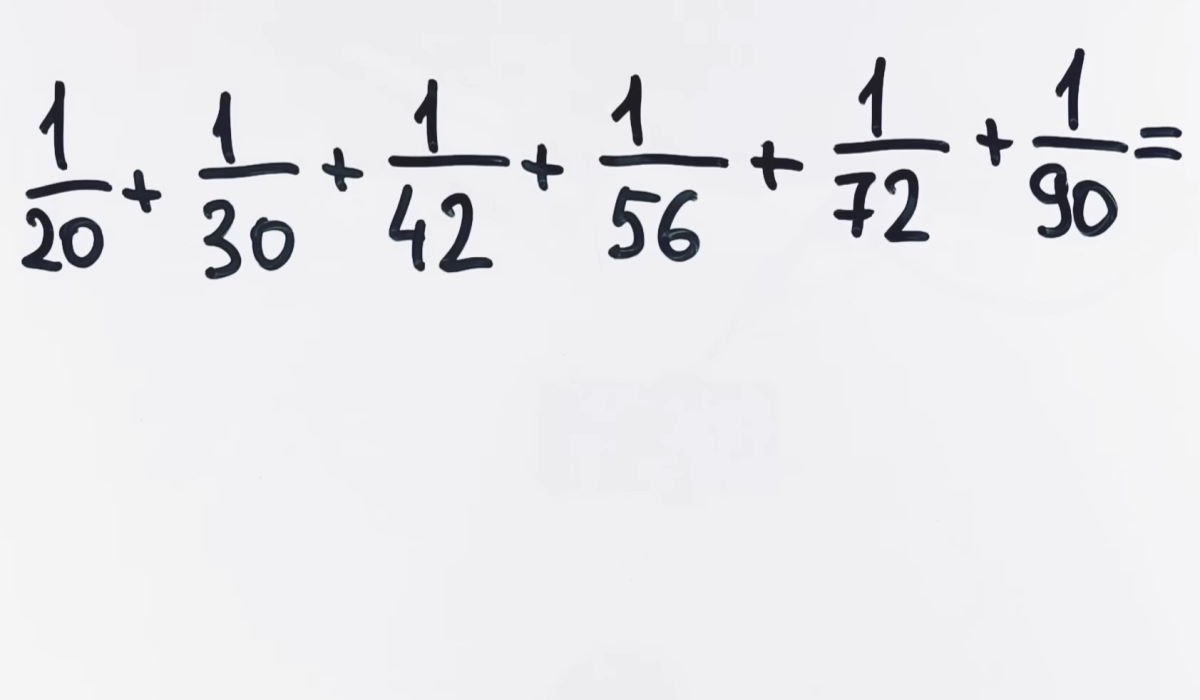
Un matemático experimentado muestra su forma de resolver. Para ello, primero descompone todos los denominadores en multiplicadores. Después de todo, los números disponibles son bastante adecuados para ello.
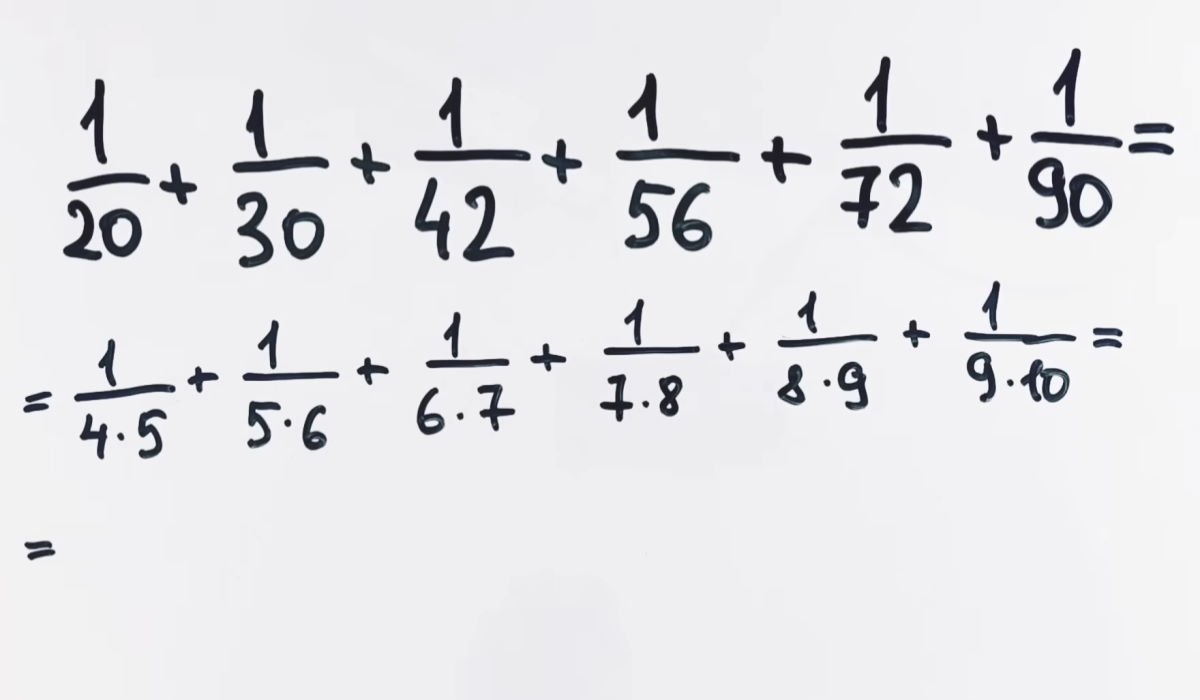
Y como en todas partes del numerador tenemos una unidad, podemos escribirla en cada caso con los mismos dígitos que tenemos en el denominador. Para ello, el primer caso será 5 – 4, luego 6 – 5 y así sucesivamente.
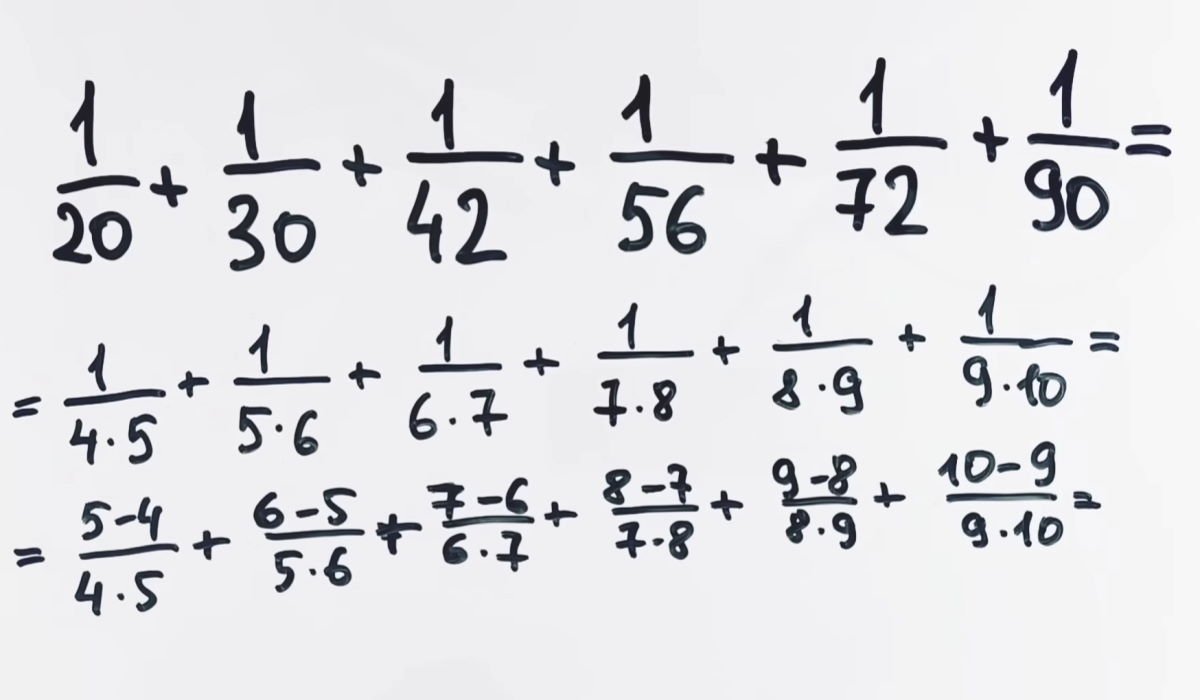
Como vemos, el ejemplo original que tenemos se ha transformado radicalmente. Sin embargo, se trata sólo de un cambio de apariencia para una solución más sencilla. Los valores siguen siendo los mismos, así que puedes seguir trabajando con la conciencia tranquila.
A continuación, el autor de la solución sugiere dividir el numerador por el denominador. Esto nos permitirá acercarnos a la solución, porque en cada fracción resultante podremos reducir algo.
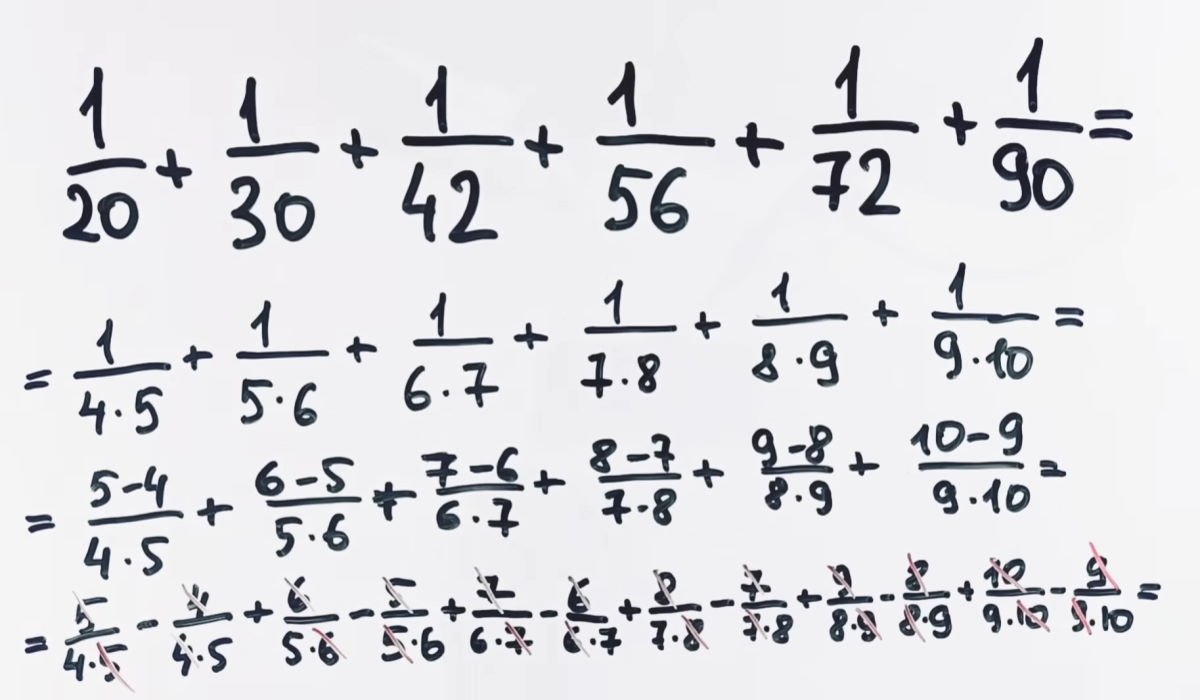
Después de tan ingeniosas manipulaciones matemáticas, obtendremos una respuesta casi lista. Queda bastante trabajo por hacer. Las fracciones disponibles tras el siguiente signo igual se reducen y dan la respuesta que hemos estado buscando todo este tiempo, que inicialmente parecía muy difícil de encontrar.

Ahora lleva todo al denominador común para obtener la fracción final. La solución resultante es preciosa. Puedes ver la solución a este problema con más detalle en el maravilloso canal «Esto no lo enseñan en el colegio».

Por supuesto, los números en esta tarea fueron seleccionados originalmente de tal manera que era posible resolver todo de una manera no estándar. Además, en tal caso hay otras formas de llegar a una solución. ¿Has conseguido resolverla? Cuéntanos cómo lo has hecho.